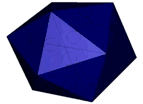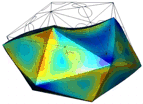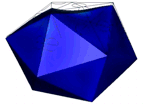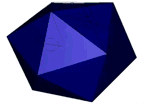
During one of our more recent projects we combined atomic force microscopy with total internal reflection microscopy to study the the genome release of viruses (Ortega-Esteban et al. 2015). This work was performed in collaboration with Pedro de Pablo (Universidad Autónoma de Madrid) and Urs Greber (University of Zurich). Currently, this correlative microscopy method is further advanced in the group of Pedro de Pablo.
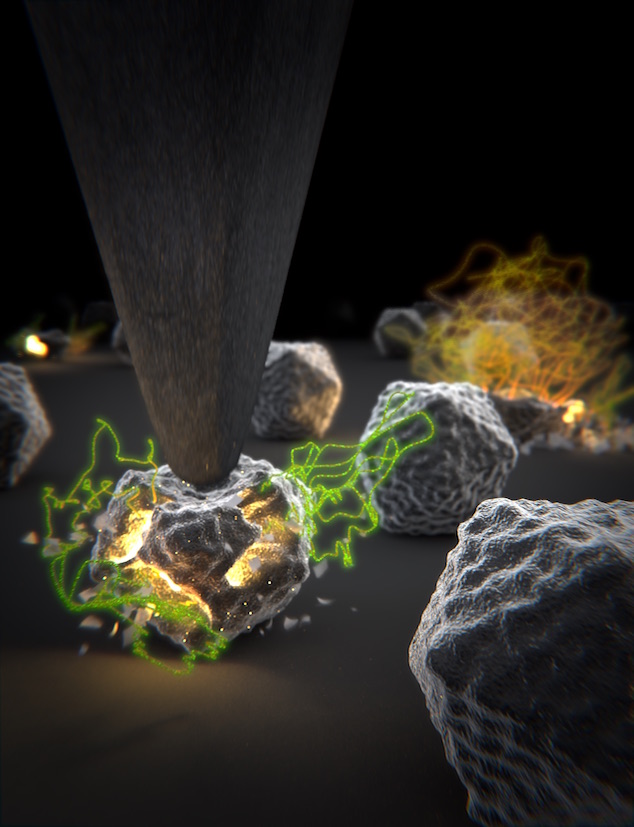
Figure 1: AFM unpacking of adenovirus
A cartoon of the experiment shows the unpacking experiment. By using Yoyo-1 as fluorescent label we can track the release of the viral DNA. The full animation can be found here.